Zand: Vaste Stof, Vloeistof of Gas?
Werkgroep 26
J.P. van der Weele & P.G. Eshuis
Physics of Fluids, Universiteit Twente
Inleiding
Granulaire — korrelvormige — stoffen kom je overal tegen. Ze worden verwerkt en toegepast in bedrijfstakken zoals de farmaceutische industrie (poeders, pillen), de mijnbouw (kolen, mineralen), de landbouw (zaden, graansilo's), de voedselproductie (suiker, meel), bouwsector (mortel, grint) en talloze andere. Volgens schatting wordt op wereldschaal 10% van de energie verbruikt door deze industrieën en gaat maar liefst 40% hiervan verloren door problemen met de verwerking en het transport van granulair materiaal [1,2]. Naast dit enorme economische belang zijn granulaire materialen ook bijzonder interessant vanuit fundamenteel wetenschappelijk oogpunt. Net als andere stoffen komen ze voor in drie verschillende fasen (vast, vloeibaar en gasvormig) maar in weerwil van deze uiterlijke overeenkomst gedraagt granulaire materie zich héél anders dan een gewone vaste stof, vloeistof of gas.
In de werkgroep kwamen onder meer de volgende drie voorbeelden aan bod.
Vaste Stof: dilatancy
Waarom kleurt het vochtige zand aan het strand wit wanneer je er overheen loopt (zie figuur 1)? Dat komt doordat het zand uitzet: als er een kracht op wordt uitgeoefend gaan de zandkorrels verder uit elkaar zitten en zakt het water weg in de hierdoor ontstane ruimte. Droog zand is lichter van kleur dan nat zand en dus wordt het zand rond je voeten lichter.
Een granulaire vaste stof zet dus uit wanneer men er een kracht op uitoefent, precies het tegenovergestelde van wat een gewone vaste stof doet! Deze speciale eigenschap heet dilatancy en werd voor het eerst opgemerkt en verklaard door de Schotse fysicus Osborne Reynolds in 1885 [3]. Op het bijgevoegde werkblad wordt het nader onder de loep genomen.
Reynolds (1885):
"A strongly compacted granular medium dilates under pressure".
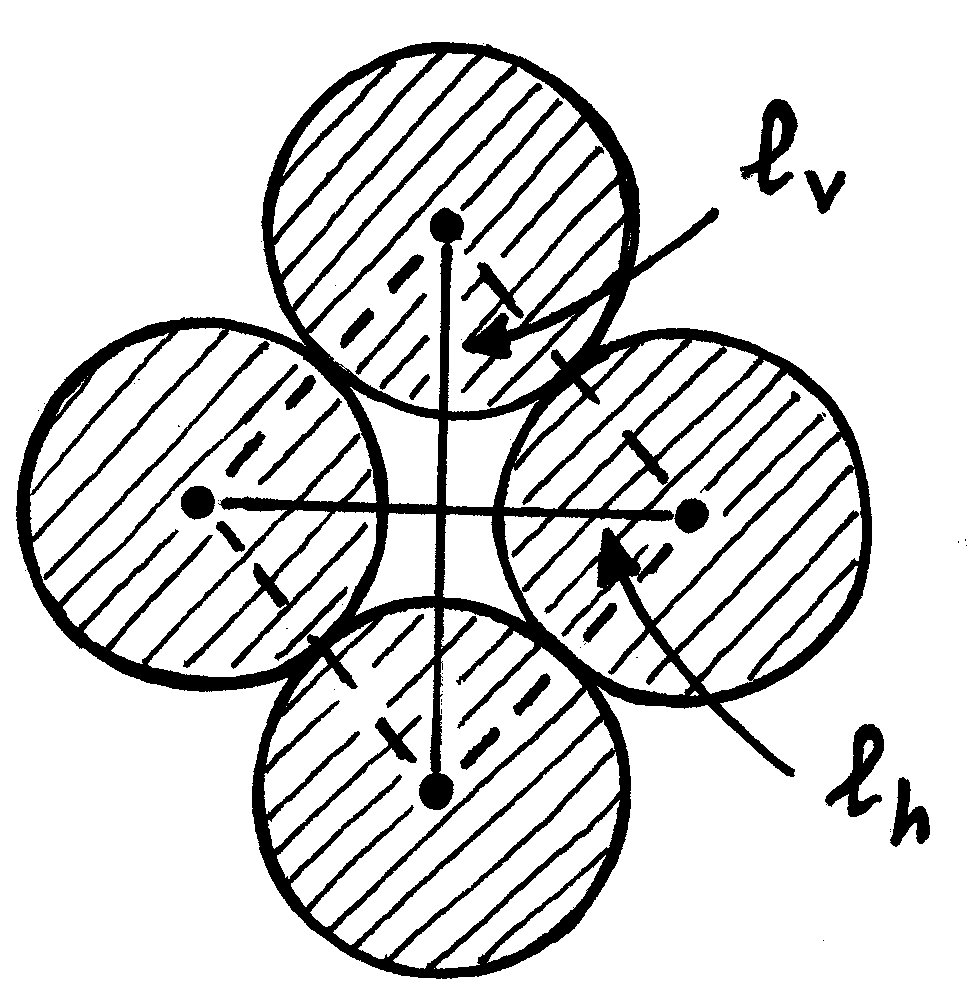
Laten we dit eens controleren aan de hand van het parallelogram hiernaast, de "eenheidscel" van een uniform 2-dimensionaal granulair medium, gevormd door vier gelijke schijven met straal R. Hoe verandert de grootte van de holte tussen de schijven als we het parallellogram indrukken?
We nemen hierbij aan dat de schijven voortdurend met elkaar in contact blijven.
- Laat zien, met de stelling van Pythagoras, dat:
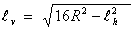 . .
- Overtuig jezelf ervan dat de oppervlakte van de holte (Aholte) gelijk is aan het oppervlak van het parallelogram min de oppervlakte van één schijf. In formule:
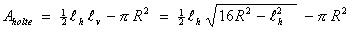 . .
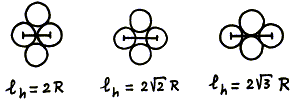
- Tijdens het indrukken gaat de eenheidscel door de nevenstaande drie stadia. Bepaal de bijbehorende drie waarden van Aholte , en schets de grafiek van Aholte als functie van ℓh.
- Conclusie: Als je erop drukt...
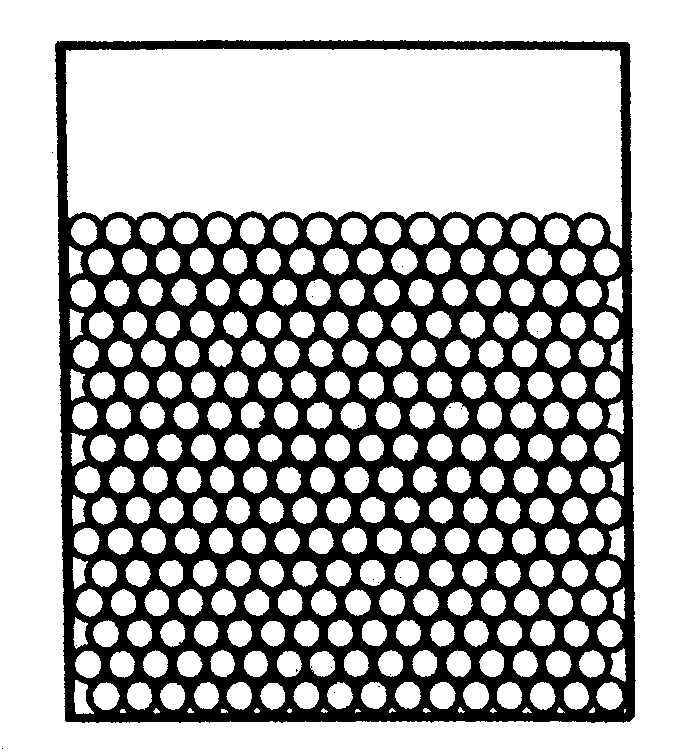
|
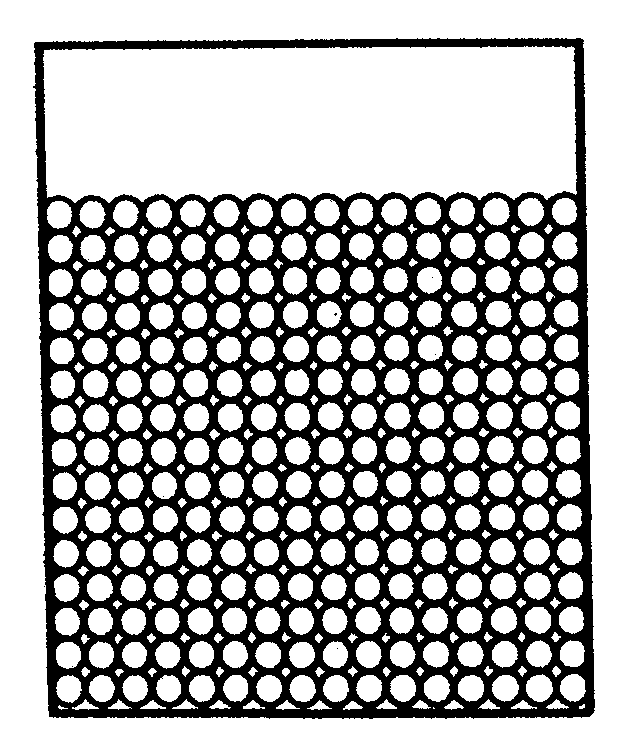
|
... zal deze bak met euro's
uitzetten of inklinken?
|
... en wat zal deze doen?
|
Wat vind je, had Reynolds gelijk met zijn uitspraak?
|
Werkblad bij de werkgroep "Zand: Vaste Stof, Vloeistof of Gas", door Ko van der Weele en Peter Eshuis, Physics of FLuids groep, Iniversiteit Twente
|
|


Fig. 1: Een bijzondere vaste stof. Waarom is er een witte ring rond je voetafdruk op het strand te zien? Deze vraag werd beantwoord door Reynolds, hier geportretteerd door John Collier.
Vloeistof: arching
Ook als zand stroomt, zoals in een zandloper, is het een fascinerende stof. De op elkaar steunende zandkorrels vormen structuren die doen denken aan Romeinse triomfbogen (het zogenaamde arching effect) die de krachten in zijwaartse richting wegleiden (zie figuur 2) [4]. Een gewone vloeistof gaat steeds langzamer stromen naarmate het bovenste compartiment leger wordt, de hydrostatische druk wordt immers steeds kleiner. In de zandloper daarentegen is deze druk niet of nauwelijks aanwezig, omdat de boogstructuren in het zand de druk van het bovenliggende zand zijwaarts wegleiden. Er staat daarom altijd dezelfde druk op het zand bij de opening, ongeacht de hoeveelheid zand in het bovenste compartiment. Hierdoor stroomt er continu evenveel zand door de zandloper.

Fig. 2: Een bijzondere vloeistof. Wat is het verschil tussen een zandloper en een waterklok? De schets in het midden laat het arching effect zien zoals dat optreedt in de zandloper: de zandkorrels die de meeste druk opvangen (zwart) vormen duidelijke boogstructuren. In de waterklok is dit effect niet aanwezig en hebben we te maken met de gebruikelijke hydrostatische druk.
In de werkgroep namen we de proef op de som. Eerst controleerden we dat er door een zandloper iedere minuut dezelfde hoeveelheid zand stroomt. Vervolgens vulden we een halve-liter petfles met 0.16 liter water, en zetten de fles omgekeerd op een maatbeker zodat het water (door een gaatje in de dop) in de beker stroomde. We maten de tijdstippen waarop de opeenvolgende markeringen op de maatbeker gepasseerd werden, en dit leverde de grafiek in figuur 3 op. Hierin is te zien dat het doorgestroomde volume steeds langzamer toeneemt naarmate het waterpeil in de petfles zakt.
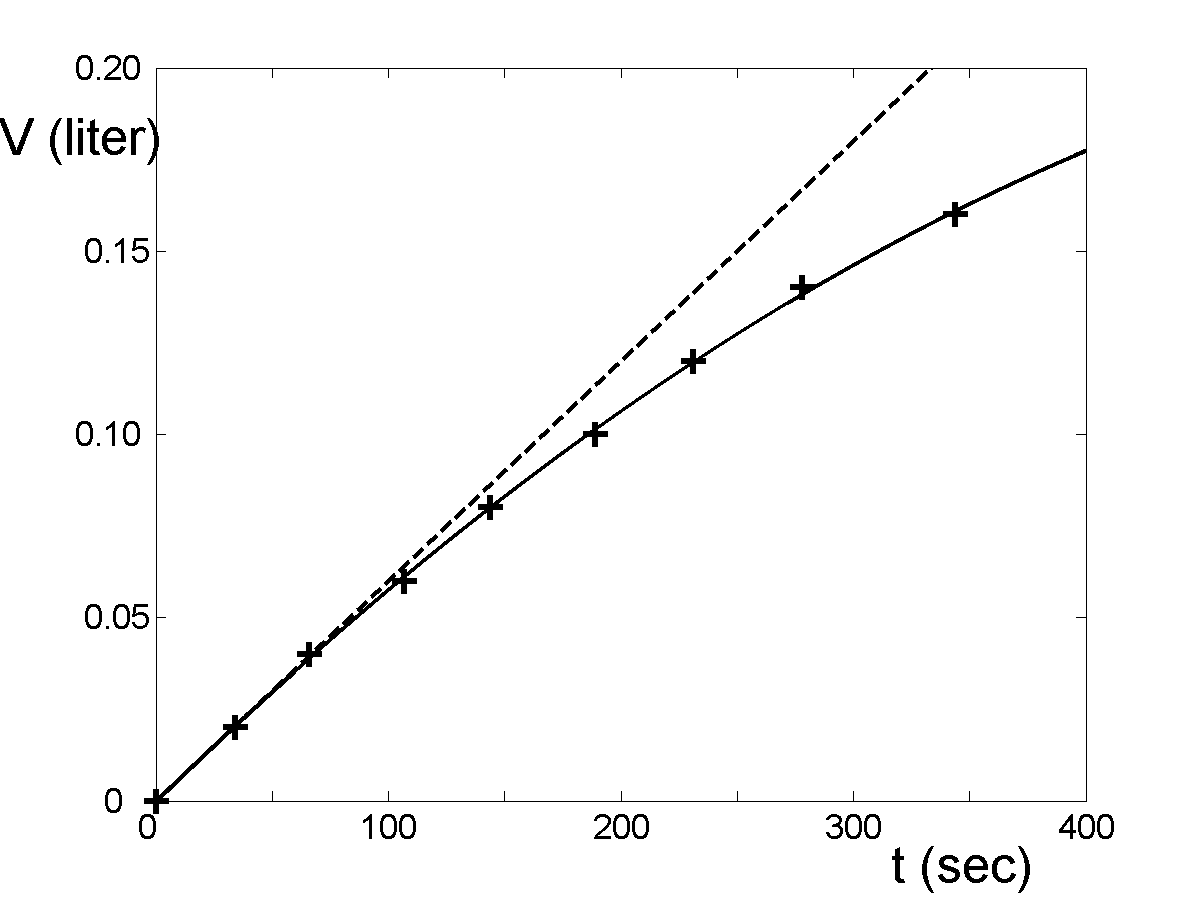
Fig. 3: Het doorgestroomde watervolume V als functie van de tijd t voor de waterklok. Voor een zandloper neemt het volume lineair toe met de tijd (stippellijn), maar voor de waterklok gaat de toename steeds langzamer wegens de afnemende hydrostatische druk (meetpunten plus fitcurve). De grafiek is gebaseerd op metingen die tijdens de werkgroep zijn gedaan.
Gas: clustering
Tenslotte kan granulair materiaal ook de gedaante aannemen van een gas. De ringen van Saturnus (bestaande uit brokstukken ijs en steen) zijn een goed voorbeeld, en ook op aarde kun je granulaire gassen creëren: schud maar eens een pot met koffiebonen op en neer. Ook in deze vorm gedraagt granulaire materie zich weer geheel anders dan de gassen waaraan we gewend zijn. Het blijkt zich namelijk niet te verspreiden over de gehele beschikbare ruimte, maar juist te clusteren!
Dit tegenintuïtieve gedrag is terug te voeren op het feit dat de onderlinge botsingen tussen de deeltjes niet geheel elastisch zijn: in elke botsing gaat een klein beetje bewegingsenergie verloren. Heel mooi is dit te zien in de opstelling van figuur 4 waarin tweehonderd fietskogeltjes, aanvankelijk evenredig verdeeld over vijf compartimenten, geschud worden. In een compartiment waar bij toeval wat meer kogeltjes zitten dan gemiddeld, vinden meer botsingen plaats en gaat er dus meer energie verloren. De kogeltjes maken elkaar hier langzamer en springen niet meer zo hoog; zie het meest linkse en middelste compartiment na 10 en 25 s. De kogeltjes kunnen nog maar moeilijk ontsnappen uit deze compartimenten, en het effect wordt nog versterkt door de kogeltjes die erbij komen vanuit de relatief lege compartimenten (waar de deeltjes juist veel hoger springen). Reeds na 25 s zijn bijna alle kogeltjes verzameld in twee clusters. Deze twee strijden vervolgens om de overwinning, waarbij het grootste cluster uiteindelijk aan het langste eind trekt [5,6].



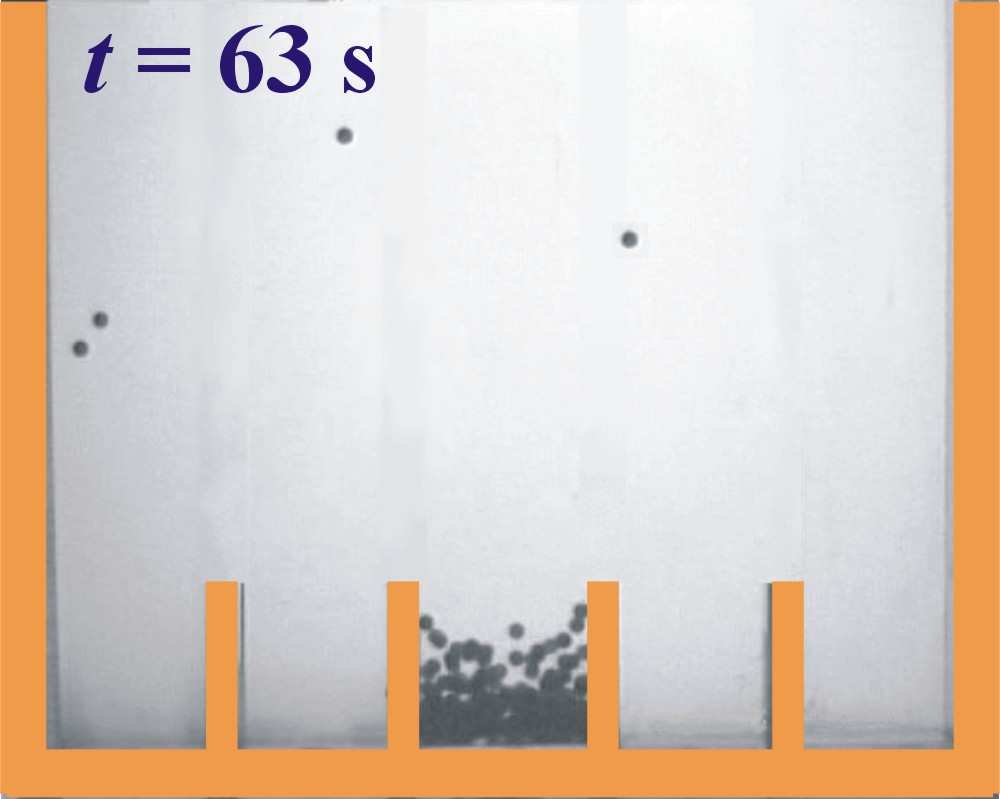
Fig. 4: Een bijzonder gas. Clusterende kogeltjes in een schudexperiment met vijf compartimenten. In de begintoestand zitten er veertig kogeltjes in elk compartiment. Vanwege de spontaan optredende scheiding in 'koude' compartimenten (met veel langzame kogeltjes) en 'warme' (met slechts enkele, veel snellere kogeltjes) wordt dit ook wel het Maxwell Demon experiment genoemd [5,6].
Tot zover enkele voorbeelden uit de rijk geschakeerde wereld van granulaire materie. Het is één van de snelst groeiende gebieden in de hedendaagse natuurkunde, en dit vertaalt zich in een explosieve toename van het aantal artikelen, met daarin steeds weer nieuwe, verrassende verschijnselen. Of het nu gaat om het Brazil-nut effect [7], wandelende duinen op aarde en Mars [8], of om het mysterieuze 'zingende zand' [9], granulaire materie is altijd fascinerend.
Referenties
[1] T. Mullin, Mixing and de-mixing, Science 295, 1851 (2002).
[2] H.M. Jaeger, S.R. Nagel, and R.P. Behringer, Granular solids, liquids, and gases, Rev. Mod. Phys. 68, 1259 (1996); see also H.M. Jaeger, S.R. Nagel, and R.P. Behringer, The physics of granular materials, Physics Today 49, 32 (1996).
[3] J. Duran, Sand, Powders, and Grains: An Introduction to the Physics of Granular Materials (Springer, New York, 2000).
[4] Zie de website http://www.phy.duke.edu/research/ltb/ltbgroup.html voor mooie experimentele figuren van het arching effect (Bob Behringer, Nonlinear Flow Group, Duke University).
[5] K. van der Weele, D. van der Meer, en D. Lohse, Clustering in granulair gas; Maxwell's duivel op de korrel genomen, Ned. Tijdschrift voor Natuurkunde 68, 22 (Jan. 2002).
[6] M. Sandtke en K. van der Weele, Maxwells duivel staat naast je in de file, Natuur en Techniek (Feb. 2002) blz 28; zie ook het corresponderende artikel van de hoofdredacteur J. van den Broek, Fascinerende fysica van fietskogeltjes, zelfde nummer, blz 76. Beide artikelen zijn verschenen op de website http://www.natuurkunde.nl.
[7] Wanneer je een notenmix schudt, komen de grootste noten (de "Brazil nuts" ofwel paranoten) bovendrijven.
Zie: http://www.vpro.nl/wetenschap/index.shtml?3626936+4257491+10287728
voor meer informatie (VPRO, Noorderlicht-wetenschapspagina).
[8] Dit zijn de befaamde Barchan-duinen, waarover veel goede websites bestaan. Zie bijvoorbeeld http://www.ica1.uni-stuttgart.de/~gerd/dunes.html (Universität Stuttgart) of http://www.marstoday.com/viewsr.html?pid=9845 (NASA Mars Global Surveyor Project).
[9] Wereldwijd zijn er enkele honderden "singing" en "booming" zandduinen bekend. Op de website http://www.schweich.com/sbdA.html worden er een aantal beschreven in Californië en Nevada.






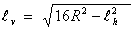 .
.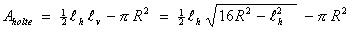 .
.