`Hebt u wel eens van
x gehoord?' Deze gedenkwaardige woorden sprak Hans Freudenthal op de
avond van 24 november 1989 in hotel De Mallejan te Vierhouten tijdens een
bijeenkomst over algebra.
De aanwezigen keken even verbaasd op:
x en algebra is toch zoiets als een twee-eenheid? De werkelijkheid is dat
er een tijd was dat nog niemand van x
gehoord had, terwijl er wel al algebra was. Er was een tijd dat uit de pen
van de statisticus beschrijvingen vloeiden, maar geen berekeningen, en zeker
geen x . Wat zit er historisch gezien
achter deze veranderingen? Wat hebben ze opgeleverd? Waar schiet de wiskund(ig)e
echt iets mee op? Over deze vragen, toegespitst op algebra en statistiek,
gaan de bijdragen in het kader van dit thema. Voor docenten, die constant
veranderingen meemaken (in de leerplannen) en hun leerlingen begeleiden, lijken
dat belangrijke vragen.
Een uitgebreide lijst met bronnen en
literatuur die betrekking hebben op dit thema wordt tijdens de Nationale Wiskunde
Dagen uitgereikt.
De met cijfers bedekte negentiende
eeuw
Ida Stamhuis
Vrije Universiteit, Amsterdam
`Theorie der Statistiek of Staats-kunde'
is de titel van een boek dat in 1807 werd uitgebracht door H.W. Tijdeman,
hoogleraar in de statistiek aan de Leidse universiteit. Voor ons is het merkwaardig
dat hij `statistiek' met `staatskunde' identificeerde en verder dat de statistiekcolleges
die hij gaf niet verplicht waren voor wiskundigen of bijvoorbeeld sociale
wetenschappers, maar wel voor juristen. Wat verstond hij eigenlijk onder statistiek?
Een woordenboek uit 1826 omschreef statistiek als volgt:
`Statenkunde, statenbeschrijving, uit
staatkundige oogpunten beschouwd. Zij (…) draagt dus den tegenwoordigen
toestand van eenen staat voor (…). Hierdoor is zij een (…) leerrijk
oefenschool voor den staatsman; alleen moet zij in geen bloot tabellenwerk
en getalregisters ontaarden.' Niet teveel getallen dus, wel relevante kennis
voor een toekomstige ambtenaar of politicus.
Statistiek was in het midden van `de
met cijfers bedekte negentiende eeuw' een modieus vakgebied. Statistische
gegevens hadden veel gezag en werden dan ook gebruikt om beweringen overtuigingskracht
te geven. De `Lady with the Lamp', ofwel Florence Nightingale, gebruikte ze
dan ook als zodanig. Ze beschouwde statistiek als de belangrijkste wetenschap
in de hele wereld, omdat het de ervaring in exacte resultaten omzet. Ze verzamelde
getallen en nog eens getallen om aan te tonen dat de sterfte onder soldaten
meer veroorzaakt werd door deplorabele hygiënische omstandigheden dan
door verwondingen op het slagveld. Om het de politici, voor wie ze haar rapporten
schreef, zo makkelijk mogelijk te maken, bedacht ze nieuwe grafische representaties
van het statistische materiaal, zodat ze in één oogopslag konden
zien waarvan ze hen wilde overtuigen.
Aan het eind van de eeuw was er de bekende
Engelse wetenschapper Francis Galton die een hartstochtelijke neiging had
om alles in getallen uit te drukken: niet alleen zoiets als hoofdomvang en
beenlengte maar hij definieerde ook een `vervelingscoëfficiënt'
of een `schoonheidscoëfficiënt'. Hij werkte met de normale verdeling:
vrouwen waren volgens hem één standaarddeviatie dommer dan mannen.
Hij kwam met het idee van correlatie en van regressie naar het gemiddelde.
Ook voor Galton was de statistiek een middel; hij wilde zijn genetische en
eugenetische ideeën hierdoor kracht bijzetten.
Zo veranderde de statistiek in de loop
van de tijd. De inhoud, die aanvankelijk heel breed was, versmalde zich. Er
ontwikkelde zich een notatie waarbij symbolen een rol gingen spelen. Het zou
echter tot in de twintigste eeuw duren voor er een vak mathematische statistiek
ontstond. Een centraal begrip werd de stochastische grootheid X, die als jongere
broer van Descartes' x kan worden beschouwd.
Cohen, I.B. (1984). Florence
Nightingale. Scientific American 250 (3), 98-107.
Diamond, M. and M. Stone (1984). Nightingale on Quetelet
(Part 1). Journal of the Royal Statistical Society A 144, 66-79.
Hacking, I. (1990). The taming of chance. Cambridge:
Cambridge University Press.
Porter, T. M. (1986). The rise of statistical thinking,
1820-1900. Princeton: Princeton University Press.
Stamhuis, I.H. (1989). Cijfers en Aequaties en kennis
der staatskrachten. Statistiek in Nederland in de negentiende eeuw. Amsterdam:
Rodopi, 295 pp.
Stamhuis, I.H. en A. de Knecht-van Eekelen (red.)
(1992). De met cijfers bedekte negentiende eeuw. Toepassing van statistiek
en waarschijnlijkheidsrekening in Nederland en Vlaanderen tussen 1840 en
1920. Themanummer van Gewina, tijdschrift voor de geschiedenis der geneeskunde,
natuurwetenschappen, wiskunde en techniek. Rotterdam: Erasmus Publishing,
78 pp.
Stigler, S.M. (1986). The history of Statistics. The
measurement of uncertainty before 1900. Cambridge: Cambridge University
Press.

De wortels van de algebra
Jan Hogendijk
Vakgroep Wiskunde, Universiteit Utrecht
Deze lezing gaat over de geschiedenis
van de kwadratische vergelijking in de Babylonische en Arabische cultuur.
De lezing is toegankelijk voor iedereen die kwadratische vergelijkingen
kan oplossen. We zullen eerst een Babylonisch kleitablet uit omstreeks 2000
voor Chr. behandelen, waarop een kwadratische vergelijking wordt opgelost.
Dit zullen we vergelijken met een gedeelte van het leerboek over algebra
van de Arabische wiskundige al-Khwarizmi (ca. 830).
Teksten en vertalingen zullen aan de
deelnemers worden uitgereikt. Ook zullen we ingaan op het feit dat de algebra
uitgebreid bestudeerd werd in zowel de Babylonische als de Arabische cultuur,
hoewel het vak geen maatschappelijke relevantie had en er nauwelijks serieuze
toepassingen van de algebra in andere wetenschappen bestonden.
Neugebauer, O. (1935-1937).
Mathematische Keilschrift-Texte, 3 delen. Berlin.
Neugebauer, O. (1957). The exact sciences in antiquity.
Providence.
Rosen, F. (ed.) (1831). The algebra of Mohammed ben
Musa (al-Khwarizmi). London.
Scholz, E. (1990). Geschichte der Algebra, eine Einfuehrung.
Mannheim: B.I. Wissenschaftsverlag.
Waerden, B.L. van der (1950). Ontwakende wetenschap.
Egyptische, Babylonische en Griekse wiskunde. Groningen.
Toen x nog een grote onbekende
was
Marjolein Kool
Domstad Akademie, Utrecht
Twee vrienden, Willem en Wouter, willen
een paard van zestig gulden kopen. `Geen punt', zegt Willem, `leen mij 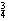 van jouw geld en ik betaal dat paard wel even.' `Nee', zegt Wouter, `leen
mij
van jouw geld en ik betaal dat paard wel even.' `Nee', zegt Wouter, `leen
mij 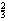 van jouw geld en ik zal het
beestje betalen.' Hoeveel geld bezaten de beide vrienden?
van jouw geld en ik zal het
beestje betalen.' Hoeveel geld bezaten de beide vrienden?
Je hoeft niet veel van wiskunde te
weten om dit vraagstukje uit het rekenmanuscript van Christianus van Varenbraken
(1523) op te kunnen lossen. Je stelt een stelsel vergelijkingen op en daar
rolt al snel het goede antwoord uit. Christianus van Varenbraken maakte
echter bij het oplossen van dit vraagstuk geen gebruik van een stelsel van
vergelijkingen; x was voor hem nog een onbekende. Daarin was hij geen uitzondering,
ook zijn zestiende-eeuwse collega's rekenboek-schrijvers losten de ingewikkeldste
vraagstukken op met `handig rekenen'. Slechts een enkele rekenmeester maakte
destijds gebruik van de Regula Cos, de algebra. Daar zal ik op het eind
van mijn lezing een voorbeeld van laten zien.
Tijdens mijn lezing ontmoeten we niet
alleen paardenkopers, we maken ook kennis met een man op zijn sterfbed,
een vrouw die bevalt van een hermafrodiet, een vrijster in een appelboomgaard
en nog vele andere curieuze hoofdrolspelers in zestiende-eeuwse vraagstukken.
Ik hoop de wiskundeleraren die naar mij komen luisteren zo te inspireren
met bizarre verhalen en fraaie staaltjes rekenkunst, dat ze net als ik af
en toe een stukje geschiedenis in hun wiskundeles zullen gaan toepassen.
Vandaar ook dat iedereen die komt luisteren een pakketje materiaal mee naar
huis krijgt.
Ik ben ervan overtuigd dat het voor
sommige leerlingen een troost zal zijn als ze ontdekken dat algebra ook
maar een keuze is geweest en dat je ook zonder x op veel vragen een antwoord
kunt vinden. Zelfs op de vraag: wat is er nou zo leuk aan wiskunde?
Arrighi, G. (1964). Trattato
d'arithmetica. Pisa.
Arrighi, G. (1969). Trattato di aritmetica. Florence.
Deschauer, S. (1992). Das zweite Rechenbuch von Adam
Ries. Braunschweig.
Flegg, G. (1985). Nicolas Chuquet: Renaissance mathematician.
Dordrecht.
Kool, M. (1988). Christianus van Varenbrakens Die
Edel Conste Arithmetica. Brussel.
The Mathematical Gazette, vol. 76, nr. 475, maart
1992.
Swets, F. (1987). Capitalism and Arithmetic: The New
Math of the 15th century. La Salle.
Tropfke, J. (1980). Geschichte der Elementarmathematik.
`Das angewandte Rechnen', p. 513-660. New York.
Vogel, K. (1954). Die Practica des Algorismus Ratisbonensis.
München.
Vogel, K. (1977). Ein italienisches Rechenbuch aus
dem 14. Jahrhundert. München.
Hebt u wel eens van z gehoord?
Jan van Maanen
Faculteit Wiskunde, Universiteit Groningen
Vergelijkingen zijn van alle tijden.
De taal waarin ze gesteld werden veranderde, van een volledige zin over
onbekende getallen tot een zin met daarin een aantal afkortingen, en van
daaruit stap voor stap tot een sliert symbolen die getallen, operaties en
relaties voorstellen. Dit proces verliep niet lineair. Zo noteerde Diophantus
(rond 250 na Chr.) machten van de onbekenden al met korte symbolen, terwijl
middeleeuwse Arabische en zestiende-eeuwse Italiaanse algebrateksten vergelijkingen
wel weer voluit schreven. Van getallenraadsels werd het algebra doordat
wiskundigen (vooral de Arabische) inzagen dat vergelijkingen in te delen
waren in typen, die elk een vaste manier van oplossen kenden of die zich
hardnekkig tegen een oplossing bleven verzetten (zoals de derdegraads vergelijking).
In de zestiende eeuw raakte de algebra
in een stroomversnelling, en dat is, na een korte terugblik op het voorafgaande,
ook het punt waarop we de draad zullen oppakken. Italiaanse rekenmeesters
deden grote stappen voorwaarts, met Cardano's Ars Magna (De Grote Kunst,
1545) en Bombelli's Algebra (1572) als hoogtepunten. De Fransman Viète
voerde aan het einde van de eeuw een consequente half-symbolische notatie
in (met A, E, I,… als onbekenden en medeklinkers als constanten),
en droeg nieuwe oplossingsmethoden en nieuwe problemen aan. De wiskunde
van Fermat was op de leest van Viète geschoold, en rond 1630 wist
Fermat dat je krommen in het platte vlak kunt voorstellen met een vergelijking
in A en E, maar hij maakte dat niet wereldkundig. Werk van Fermat circuleerde
in handgeschreven kopieën, maar alleen voor de incrowd.
Anders was het met het wiskundige werk
van Descartes. Als dat niet zo was geweest had onze huidige wiskunde er
misschien wel heel anders uitgezien! In Descartes' verhandeling uit 1637
over het verband tussen algebra en meetkunde, kortweg Géométrie
geheten, vinden we het antwoord op de vragen: waar komt onze x vandaan,
waarom is die ingevoerd? Merkwaardig genoeg was er, voordat de x opdook,
bij Descartes eerst een z, want consequent als hij was in het kiezen van
constanten uit het begin van het alfabet en variabelen uit het eind, nam
Descartes voor problemen met één onbekende in de Géométrie
voor de onbekende aanvankelijk de letter z.
We gaan dat allemaal van dichtbij bekijken.
Het meeste zal verteld worden aan de hand van oorspronkelijke teksten uit
die tijd, zodat iedereen zich een beetje historicus kan voelen en terug
op school de jeugd zal kunnen berichten over resultaten van eigen `onderzoek'.
Deelnemers aan deze werkgroep krijgen
een uitgebreide literatuurlijst uitgereikt. De lijst is samengesteld voor
gebruik in de bibliotheek van het Mathematisch Instituut van de Universiteit
Utrecht (Budapestlaan 6, De Uithof), maar veel boeken zullen ook in andere
bibliotheken te vinden zijn.
Maanen, J.A. van (1989).`avant
la lettre'. In: A.W. Grootendorst (ed.), Vacantiecursus 1983. Complexe getallen.
CWI Syllabus 15, Amsterdam, pp 1-24.
Maanen, J.A. van (1987). Facets of seventeenth century
mathematics in The Netherlands. Dissertatie Utrecht.
Scholz. E. (Ed.) (1990). Geschichte der Algebra.
Eine Einführung. Mannheim.
Smith, D.E. & M.L. Latham (Eds.) (1954). The Geometry
of René Descartes. With a facsimile of the first edition. New York.
Thema wiskunde om de wiskunde
Getaltheorie is ontstaan uit nieuwsgierigheid
naar de eigenschappen van de getallen 1, 2, 3, 4, 5, ... Of, zoals Brouwer
het formuleerde in zijn dissertatie:
`Een, twee, drie, ... zo begint de wiskunde;
wellicht in de ontwikkeling van de mensheid, wellicht in de ontwikkeling van
het kind.'
Een bijzonder aspect van de getaltheorie
is het feit dat zowel `professionals' als `amateurs' zich door de tijden heen
met groot enthousiasme op dit vakgebied binnen de wiskunde gestort hebben.
Alleen dat feit al maakt dit onderwerp buitengewoon geschikt voor de Nationale
Wiskunde Dagen. De reden dat amateurs en leken zich zozeer door getaltheorie
voelen aangetrokken ligt vooral ook in het feit dat de problemen zo voorstelbaar
zijn. Dat geldt in aanmerkelijk mindere mate voor de oplossingen. De stelling
van Fermat is hier een goed voorbeeld van.
Tot het midden van onze eeuw werd getaltheorie
beschouwd als de zuiverste van de wiskundige disciplines. Dat is nu definitief
voorbij. Getaltheorie is door de opkomst van digitale technieken een vak geworden
met vele toepassingen. Anderzijds hebben computers het mede mogelijk gemaakt
dat getaltheoretici onwaarschijnlijk grote ontbindingen in factoren hebben
kunnen uitvoeren en reusachtige priemgetallen hebben kunnen vinden.
De lezingen over dit thema zullen iets
laten zien van de fascinatie die getaltheorie kan oproepen. Onder andere de
meest recente stand van zaken rond het bewijs van de stelling van Fermat zal
aan de orde komen.
Van der Blij sprak in zijn afscheidscollege
niet zonder reden van het `Wonder-Raadselrijk der Getaltheorie'.
In en om de theorie van derdegraads
vergelijkingen
Jaap Top
Faculteit Wiskunde, Universiteit Groningen
Onder `derdegraads vergelijkingen' zullen
we met name verstaan vergelijkingen van de gedaante y = x3 + ax2 + bx + c,
in de onbekenden x en y, voor vaste a, b en c. Hierbij eisen we dan ook nog,
dat het gegeven derdegraads polynoom in x geen meervoudige nulpunten heeft.
Zowel binnen (in) de theorie hierover,
als vanuit (om) die theorie hebben recent nogal wat ontwikkelingen plaatsgevonden.
We hopen dit aan de hand van een tweetal voorbeelden te illustreren.
Een voorbeeld binnen de theorie: hoewel
misschien niet de belangrijkste ontdekking op dit gebied gedurende de afgelopen
tien jaar, levert een resultaat van J.-F. Mestre (1991) hier een fraai voorbeeld.
Het resultaat zegt iets over hoe ingewikkeld de verzameling oplossingen in
rationale getallen x en y kan zijn, wanneer de a, b, c ook rationaal gekozen
waren. Men kan namelijk uit gegeven oplossingen nieuwe construeren door de
verzameling van alle oplossingen te zien als een kromme in het x, y-vlak,
en dan lijnen in dat vlak die twee punten op de kromme verbinden opnieuw te
snijden met de kromme. (Al met wiskunde uit de derde en vierde klas kunnen
met het genoemde proces heel ingewikkeld ogende oplossingen gemaakt worden!).
Ruim zeventig jaar geleden is aangetoond
dat er altijd een eindige verzameling punten met rationale coördinaten
bestaat, zodat alle overige punten met het zojuist beschreven proces hieruit
te construeren zijn. Mestre toont aan dat er voor oneindig veel essentieel
verschillende tripels a, b, c in dit proces tenminste twaalf `beginpunten'
nodig zijn. Het bewijs berust in wezen op dezelfde technieken waarmee Fermat
in de zeventiende eeuw oplossingen van analoge vergelijkingen construeerde,
en dat is op zijn beurt in feite niets anders dan de techniek van het `kwadraat
afsplitsen' die ons in de onderbouw van de middelbare school wordt aangeleerd.
Als voorbeeld van een toepassing wordt
in het kort iets over het ontwerpen van fouten-verbeterende codes verteld.
De Laatste Stelling van
Fermat (Syllabus uitgegeven in 1993 door het Wiskundig Genootschap in samenwerking
met de Universiteit Utrecht).
Silverman, J.H. and J.
Tate (1992). Rational Points on Elliptic Curves. Springer Verlag.
Gladde getallen
Rob Tijdeman
Vakgroep Wiskunde, Universiteit Leiden
Professor Lenstra houdt een hoofdvoordracht
over het ontbinden in factoren van grote getallen. Bij het schatten van
de rekentijd van daarbij gebruikte methoden spelen `gladde getallen' een
belangrijke rol. Een natuurlijk getal wordt glad genoemd als het samengesteld
is uit kleine priemfactoren. Een manier om gladde getallen te tellen is
met behulp van de functie ψ(x,y), dat is het aantal van positieve gehele
getallen kleiner of gelijk aan x die geen priemdelers groter dan y hebben.
Zo geldt ψ(20,3) = 10, want het gaat hier om de getallen 1, 2, 3, 4,
6, 8, 9, 12, 16 en 18. De raadselen van het gedrag van ψ(x,y) zijn
in de loop van deze eeuw ontrafeld door onder andere Dickson, De Bruijn
en Hildebrand. In de voordracht worden de hoofdresultaten genoemd.
Tien jaar geleden drong het door dat
ook het produkt van de verschillende priemfactoren van een getal, de zogenaamde
radicaal, belangrijke informatie geeft. De radicaal van 100 is 10 (= 2 ×
5), de radicaal van 99 is 33 (= 3 × 11) en die van 91 is 91 (= 7 ×
13).
In de voordracht zullen enkele plaatjes
over de verdeling van radicalen worden getoond. Vermoed wordt dat als de
getallen a en b niet door hetzelfde priemgetal deelbaar zijn en beide een
kleine radicaal hebben, de som a + b een grote radicaal heeft. Als dit vermoeden
in geschikte vorm bewezen wordt, is tegelijkertijd de laatste stelling van
Fermat en nog veel meer bewezen. Ook dit verband wordt in de voordracht
gelegd. De vereiste voorkennis is wiskunde op het vwo 5-niveau.
De Laatste Stelling van
Fermat (Syllabus uitgegeven in 1993 door het Wiskundig Genootschap in samenwerking
met de Universiteit Utrecht).
Vergelijkingen in de gehele getallen
Frits Beukers
Vakgroep Wiskunde, Universiteit Utrecht
Beschouw de vergelijking x2 - 5y2 =
1 met als bijzonderheid dat we alleen naar geheeltallige oplossingen x,
y kijken. Eén oplossing ziet u waarschijnlijk meteen: x = 1, y =
0. Zijn er nog meer? Na enig zoeken vinden we x = 9, y = 4. Het blijkt zelfs
dat we oneindig veel oplossingen kunnen vinden. Vergelijkingen waarbij we
de onbekenden geheel veronderstellen noemen we diophantische vergelijkingen,
naar de Griek Diophantos die ze voor het eerst systematisch bestudeerde.
De restrictie `geheeltallige oplossing' maakt het altijd tot een verrassing
of een diophantische vergelijking wel of geen, of misschien oneindig veel
oplossingen heeft. Vorig jaar heeft Andrew Wiles bewezen dat als n >
2, de vergelijking xn + yn = zn geen oplossing in positief gehele x, y,
z heeft. Hiermee werd een notoir 350-jarig probleem van Fermat opgelost.
Wij zullen diophantische vergelijkingen van de vorm x2 + y3 = z7 of x2 +
y3 = z5 iets nader bekijken. We zullen daarbij uitleggen waarom er zo'n
groot verschil bestaat tussen deze twee genoemde vergelijkingen.
Recente geschiedenis van de laatste
stelling van Fermat
Bart de Smit
Vakgroep Wiskunde, Erasmus Universiteit,
Rotterdam
De laatste stelling van Fermat, die
eigenlijk ``het vermoeden van Fermat'' zou moeten heten, zegt dat voor geen
enkel geheel getal n > 2 er positieve gehele getallen a, b en c bestaan
zodat an + bn = cn.
Het vinden van een bewijs hiervoor
is al 3 eeuwen één van de grootste uitdagingen in de wiskunde.
De moderne getaltheorie is voor een belangrijk deel ontstaan uit pogingen
om dit vermoeden te bewijzen.
Gerd Faltings heeft in 1983 een zeer
algemeen resultaat bewezen, dat impliceert dat er voor vaste n > 2 maar
eindig veel drietallen (a,b,c) bestaan waarvoor geldt dat ggd(a,b,c) = 1
en an + bn = cn.
In juni 1993 kondigde Andrew Wiles
aan, dat hij de laatste stelling van Fermat kon bewijzen. Hij had er zeven
jaar in stilte aan gewerkt. Het manuscript werd echter geheim gehouden,
en in december 1993 trok Wiles zijn claim weer in. Nu ziet het ernaar uit
dat hij met hulp van Richard Taylor zijn bewijs gerepareerd heeft.
In oktober 1994 is de tekst van deze
nieuwe versie van het bewijs openbaar gemaakt.
Het is zeer gecompliceerd en het gebruikt
veel geavanceerde resultaten uit de literatuur.
Het doel van deze voordracht is om
met elementaire middelen een indruk te geven van de ideeën die aan
het bewijs ten grondslag liggen.
Niet thema-gebonden presentaties
Naast de vijf thema's zijn er ook acht
sessies die niet gebonden zijn aan een van deze thema's. Deze werkgroepen
en presentaties zijn verdeeld in twee categorieën. De eerste betreft
de discipline wiskunde en sessies in de tweede categorie gaan over wiskundeonderwijs.
Virussen en computers
Henk Barendregt
Katholieke Universiteit, Nijmegen
CWI, Amsterdam
Virussen zijn moleculen die zichzelf
reproduceren wanneer ze zich binnen een levende cel bevinden. Hierdoor wordt
de stofwisseling van de cel verstoord.
In veel gevallen zal het immuunsysteem
van de cel het virus onschadelijk maken. Wanneer het virus echter het immuunsysteem
zelf verstoort, is dit soms niet mogelijk.
Beide soorten virussen komen (in de vorm
van software) ook voor in de wereld van computers. Aangetoond zal worden dat
er geen universele remedie tegen bestaat.
Wiskunde, een geesteswetenschap
S.J. Doorman
Faculteit Wijsbegeerte, Erasmus Universiteit
Rotterdam
Wiskunde wordt meestal als vanzelfsprekend
tot de β-wetenschappen gerekend. Ook het onderwijs in de wiskunde is
doordrenkt van deze opvatting en helpt derhalve mee haar te bevestigen.
Tegen deze achtergrond zal worden getracht
aannemelijk te maken dat het aanbeveling verdient wiskunde op te vatten als
een α-wetenschap.
Discrete analyse
H.J.A. Duparc
Technische Universiteit Delft
Het gedrag van geleidelijk veranderde
verschijnselen v = v(t) kan vaak nuttig worden beschreven met behulp van de
afgeleide  , soms met groot nut
ook wel geschreven als Dv. In analogie daarmee kunnen de lotgevallen van discreet
veranderende verschijnselen v = vn vaak nuttig worden beschreven met behulp
van de differentie-operator Δ:
, soms met groot nut
ook wel geschreven als Dv. In analogie daarmee kunnen de lotgevallen van discreet
veranderende verschijnselen v = vn vaak nuttig worden beschreven met behulp
van de differentie-operator Δ:
Δvn = vn+1 − vn.
Het is boeiend, leerzaam en nuttig om
de overeenkomst en het verschil tussen de operatoren D en Δ te bestuderen.
Het blijkt voorts nuttig om naast de operator Δ ook de operator E met
effect Evn = vn+1 in te voeren. Men heeft dan Δ = E − 1; E = Δ
+ 1.
Vier kernonderdelen van de continue analyse
hebben hun pendant in de discrete analyse volgens onderstaand staatje:
|
I
|
differentiëren
|
differentie nemen
|
|
II
|
integreren
|
sommeren
|
|
III
|
differentiaalvergelijkingen
|
differentievergelijkingen
|
|
IV
|
Laplace-transformaties
|
z-transformaties
|
Opgemerkt dient nog te worden dat differentievergelijkingen
(relaties tussen een functie v en haar differenties Δv, Δ2v, …)
kunnen worden herschreven als relaties tussen vn , vn+1, vn+2 , … en
dus te beschouwen zijn als recurrente relaties.
Doordat bij de operator Δ, in tegenstelling
tot de operator D, het limietbegrip geen rol speelt, zijn sommige afleidingen
enerzijds eenvoudiger, anderzijds zijn bepaalde formules mede daardoor ingewikkelder.
Vooraf aan de werkgroep wordt een aantal
problemen uitgedeeld die bovengenoemde problematiek illustreren.
Invloed, conflict en contact in
de meetkunde
Dirk Siersma
Vakgroep Wiskunde, Universiteit Utrecht
- Hoe verdeelt men visserijzones
tussen een aantal eilanden in de zee?
- Wat is de dichtstbijzijnde planeet
in de ruimte?
- Wat is de opdeling van Nederland
in provincies als we de afstand tot de provinciehoofdstad minimaal nemen?
Wiskundig bekijken we afstanden tot diverse
objecten in het vlak of de ruimte (punten, lijnen, cirkelschijven, bollen,
eilanden in de zee). Punten die dichter bij een object A liggen dan bij andere
objecten behoren tot de invloedsfeer van A. De randen ervan zijn de conflictgebieden.
Voorbeelden leveren als conflictverzamelingen:
middelloodlijnen, bissectrices, parabolen, zadelvlakken, enzovoort. Daarnaast
komen `drielandenpunten' veelvuldig voor, maar soms ook ingewikkelder conflictpunten.
Er zijn verbanden met ingeschreven en
omschreven cirkels, de cirkels van Apollonius, maar ook met Voronoi-betegelingen
in het vlak, enzovoort.
Kun je op computeralgebra rekenen?
André Heck
Expertisecentrum Computer Algebra Nederland,
Amsterdam
Het ultieme doel van computeralgebra
is het automatiseren van wiskunde. De hiervoor benodigde software, bekend
onder de naam computeralgebra-systeem, is bedoeld als werkomgeving voor het
uitvoeren van wiskundige en technische berekeningen. Binnen zo'n moderne werkomgeving
krijgen symbolisch rekenen, numeriek rekenen, grafiek, documentatie en aansluiting
met andere software grote aandacht.
In deze presentatie gaan we met de vraag
`Wat heb ik nu aan computeralgebra?' in het achterhoofd, in op aspecten van
gebruik van een computeralgebra-systeem als werkomgeving. Niet alleen de kwaliteit
van de geleverde wiskunde komt aan bod via concrete voorbeelden, maar ook
het bedieningsgemak en de vraag voor welke problemen de gebruiker en de softwaremaker
zich vanuit verschillend perspectief gesteld zien.
Bij gebruiksaspecten kunt u denken aan
zaken als: Hoe behoud ik overzicht over een formule, hoe vereenvoudig ik wiskundige
formules, hoe manipuleer ik een onderdeel van een formule, hoe omzeil ik automatische
vereenvoudigingen?
In[1] := Sin[a+b+c] /. Sin[x-+y-]
-> Sin[x]Sin[y] + Cos[x]Sin[y]
Out[1] = Cos[a] Sin[b+c] + Sin[a] Sin[b+c]
In[2]: = Sin[a+b+c] //. Sin[x-+y-] -> Sin[x]Sin[y] + Cos[x]Sin[y]
Out[2] = Cos[a] (Cos[b] Sin[c] + Sin[b] Sin[c]) +
> Sin[a] (Cos[b] Sin[c] + Sin[b] Sin[c])
Mag het een beetje inspirerend zijn?
Nora Blom, Hogeschool van Amsterdam,
Amsterdam
Regien Bosman, Zernike College, Groningen
Mevrouw Rose Flower werd in Engeland
in 1991 uitgeroepen tot `Maths Teacher of the Year'. Op het prikbord in haar
klas hangen prachtige symmetrische figuren. Daartussen hangt een bordje met
de uitspraak van - alweer - de Engelse wiskundige G.H. Hardy:
A Mathematician, like a Painter or a
Poet, is a Maker of Patterns.
Dat is een uitspraak die wij van harte
onderschrijven. Nu een groter beroep wordt gedaan op de zelfstandigheid van
leerlingen, `de leerlingen aan het werk', wordt de rol van de docent meer
voorwaarden-scheppend. De aankleding van het lokaal, de keuze van de leerstof
en het werken met materiaal zijn daarbij belangrijke elementen. Het zijn de
voorwaarden die ervoor zorgen dat de leerling met plezier werkt en dat er
wat geleerd wordt.
Sommige scholen hebben keuze-uren: uren
waarop leerlingen kiezen welk vak ze volgen en met welk onderwerp ze daarin
bezig willen zijn. In dit keuze-uur van deze wiskundedagen kiezen wij voor
het onderwerp: Regelmaat en Symmetrie. Een onderwerp dat een beroep doet op
het gevoel voor schoonheid binnen het vak wiskunde. Wij zullen onder andere
ingaan op de volgende vragen:
- wat is er in dit opzicht gebeurd
op de basisschool?
- hoe pak je de draad weer op
in klas 1?
- hoe laat je een leerling in
klas 4 vbo/mavo een werkstuk maken over dit onderwerp?
Kortom, wordt er op school voldoende
aandacht besteed aan de esthetische kant van wiskunde?

Albern, K. e.a. The language
of pattern.
Bain, G. Celtic Art.
Bourgoin, J. Arabic geometrical
pattern and design.
Fäustler, A. Perspectief
en projectie.
Hildebrandt, S. en A. Tromba
(1985). Natuur en techniek. Maastricht / Brussel.
Jansen, P. en R. Kock.
Informatica met logo. Enschede: SLO.
Lauwerier, H. (1988). Symmetrie.
Amsterdam: Aramith Uitgevers.
Lauwerier, H. Fractals.
Lawler, R. Sacred geometry.
Locher, J. L. Leven en
werk van M.C. Escher.
Meeder, M. e.a. (1987).
Vriendelijke wiskunde. Amsterdam: Werkgroep Vrouwen en Wiskunde.
Meeder, M. en H. Verhage
(1989). Regelmaat en symmetrie (leerlingenmateriaal en docentenhandleiding).
Utrecht / Enschede: Freudenthal instituut / SLO.
Speltz, A. The styles of
ornament.
Wiskunde en beroep
Bernadette van den Anker
SG Echnaton, Almere
`Welke wiskunde heb je later nodig?',
`Wat moet ik hier nu mee?' Het zijn vragen die iedere docent vroeg of laat
te beantwoorden krijgt.
In deze workshop worden geen antwoorden
op deze vragen gegeven, maar hooguit aanwijzingen die te maken hebben met
de toekomst van de wiskundeleerling. Het gaat om keuzebegeleiding in de
les. Voor de leerling staat de volgende vraag centraal:
Welke wiskunde heb ik nodig in mijn
toekomstig beroep?
De lessen die daarvoor geschreven zijn,
zijn gebaseerd op materiaal dat ontwikkeld is door `Vrouwen en Wiskunde'.
Deze lessen zijn dit schooljaar gegeven in de tweede klas van een brede
scholengemeenschap.
Het materiaal is geschikt voor leerlingen
van ivbo tot en met vwo.
Computernetwerken. Niets voor
het onderwijs?
Sieb Kemme, Lettelbert
Han Hermsen, Freudenthal instituut,
Universiteit Utrecht
In deze presentatie wordt met demonstraties
ingegaan op de mogelijkheden die computernetwerken het onderwijs al te bieden
hebben en in de toekomst zouden kunnen gaan bieden.
Sieb Kemme introduceert en demonstreert
de SLO-lijn, een door de Stichting Leerplanontwikkeling beheerd bulletin
board annex elektronische brievenbus voor het onderwijs.
- hoe werkt het? wat zit erin?
is er iets over wiskunde?
- hoe krijg je het eruit? wat
kun je ermee?
Han Hermsen gaat in op recente ontwikkelingen
als:
- met World Wide Web het Internet
op;
- het gebruik van Internet door
scholen in de Verenigde Staten;
en op de toekomst:
- de rol die netwerken kunnen
gaan spelen bij het inpassen van (multimediale) informatietechnologie
in het onderwijs zonder de beperkingen van nu.
Computernetwerken. Niets voor het onderwijs?
Dat hangt ervan af!
Je hebt er pas wat aan als je er op
een makkelijke manier dingen mee kunt doen die je zinvol vindt voor het
onderwijs. Denk aan:
- proefwerkopgaven en elektronische
post uitwisselen met collega's;
- op het netwerk beschikbare
gegevens gebruiken in de les;
- educatieve software of andere
gegevens via het netwerk naar je computer `downloaden'.
Technisch is het allemaal mogelijk,
in de praktijk zijn dergelijke faciliteiten beschikbaar, maar van breed
georganiseerd gebruik is nog geen sprake, waardoor de waarde ervan betrekkelijk
blijft.
Sinds jaar en dag zijn er bulletin
boards voor het onderwijs. De SLO-lijn is er een voorbeeld van. Alles wat
je nodig hebt is: een computer, een telefoonlijn, een modem, het telefoonnummer
van het bulletin board en een programma op je computer om in een tijdelijk
mini-netwerk met de bulletin board computer te kunnen communiceren. Zie
hierboven wat je vervolgens zou kunnen gaan doen.
Het is te verwachten dat de bestaande
bulletin boards gaandeweg zullen worden geïntegreerd in een modern
netwerk als Internet met nog veel meer mogelijkheden. Via een fraaie bediening
kun je gedigitaliseerde informatie (tekst, al dan niet bewegend beeld, geluid)
op allerlei terrein vanuit binnen- en buitenland op je computer afspelen.
Op dezelfde manier als bij een bulletin board ben je via één
Internet-computer verbonden met alle Internet-computers in de wereld.
Wellicht zijn er docenten die nu al
op Internet ergens iets tegenkomen dat in de les kan worden gebruikt. Voor
de enkeling die deze `digitale snelweg' kan bereizen, zijn dit soort toevalstreffers
misschien wel de spannendste dingen die je kunnen overkomen.
Computernetwerken zullen in de toekomst
echter pas werkelijk betekenis krijgen voor het onderwijs als geheel, als:
- op die netwerken iets door
en voor het onderwijs wordt georganiseerd;
- de gebruiker op een school
met kennis van zaken op een moderne en makkelijke manier door het netwerk
kan navigeren en gebruik kan maken van de geboden faciliteiten;
- elke school in staat is om
op zo'n netwerk aansluiting te vinden, waardoor een Nederlandse tak van
een mondiaal educatief netwerk kan ontstaan.
Wat moet er nog gebeuren om zover te
komen?
Hoogtemeters
Fried den Ouden
Grensland College, Budel
In het nieuwe leerplan wiskunde voor
vbo/mavo en de onderbouw havo/vwo is ruimte gereserveerd voor Geïntegreerde
Wiskundige Activiteiten (GWA). Het is de bedoeling dat leerlingen datgene
wat ze tijdens de wiskundelessen geleerd hebben, leren gebruiken en toepassen
in alledaagse situaties. Omdat er weinig of geen concrete richtlijnen zijn,
zal iedereen naar eigen inzicht een invulling geven.
In deze workshop laten we de deelnemers
kennis maken met het ontstaan en de uitvoering van zo'n GWA-project. Aan
de orde komen:
- aanleiding en opzet project;
- keuze maken uit verschillende
meetmethodes;
- hoe zelf eenvoudige meetinstrumenten
te vervaardigen;
- maken van leerlingenwerkbladen;
- mogelijk zelf metingen verrichten;
- bekijken beeldverslag van
het project;
- mogelijke uitbreiding met
moeilijker instrumenten.
De deelnemers aan de workshop krijgen
een reader uitgereikt waarin opgenomen: de totstandkoming van het project,
de leerlingenwerkbladen, een verslag van de uitvoering en een evaluatie
van het geheel. De reader omvat ongeveer 25 bladzijden.
Overige activiteiten
De Nationale Wiskunde Dagen zijn in de
belangrijke mate bedoeld als ontmoetingsplaats. De koffie-, thee- en lunchpauzes
zijn met opzet ruim gepland, zodat u van gedachten kunt wisselen met collega's.
Het Leeuwenhorst Congres Centrum biedt bovendien voldoende rustige hoekjes
om u terug te trekken om samen met een collega over de wiskunde en het wiskundeonderwijs
te praten.
Naast de thema's en lezingen die buiten
de thema's vallen is er op de Nationale Wiskunde Dagen nog veel meer te zien
en te beleven. Op vrijdagavond is er feest met live muziek en zaterdagochtend
wordt er voor de liefhebbers nog een fun run georganiseerd.
Muziek in het café
Ingrid Souren zingt met pianobegeleiding
in de lounge bij het èf-café van 22.00 tot 24.00 uur. Ingrid
Souren zingt zo'n beetje alles: chansons, ballads, rock, klassiek, ... Ze
kan putten uit een veelzijdig repertoire. Voor deze gelegenheid hebben wij
haar gevraagd bescheiden achtergrondmuziek te zingen. U mag daar doorheen
praten.
Rock & roll
In de pre rock 'n roll dagen van eind
jaren veertig, begin jaren vijftig, weten rhythm & blues sterren als Tiny
Bradshaw, Big Joe Turner, Buddy Johnson en Louis Jordan met hun wervelende
en energieke show elke zaal op zijn kop te zetten.
Ruim veertig jaar later zwepen de Gigantjes
het publiek op met dezelfde aanstekelijke muziek. De band weet daarbij precies
dezelfde sfeer neer te zetten als de helden in die tijd.
De Gigantjes zijn begonnen in 1984 als
hobby-band bestaande uit muzikanten die hun sporen in de muziek ruimschoots
verdiend hebben. Met de komst van zangeres Mieke kreeg de band een eigen gezicht.
Al gauw groeiden de Gigantjes uit tot een van de meest gevraagde live-acts
van Nederland.
De groep staat garant voor een avondvol
vaart en variatie. Muziek met een hoog entertainmentgehalte. Blijf daar maar
eens bij zitten.
De Gigantjes treden op van 23.00 tot
1.00 in de Rotondezaal.
Mieke Stemerdink zang Sjoerd Plak gitaar
Rob Kruisman saxofoon Fred van Straaten
trompet
Rob Brondsema bas Peter Paul Everts piano
& keyboard
Pete Dobson drums
Fun run
Speciaal voor degenen die vrijdagavond
niet gedanst hebben of anderszins een fysieke inspanning hebben gepleegd,
alsmede voor diegenen die stramme leden hebben overgehouden aan de vrijdagavond,
en in het bijzonder voor hen die willen aantonen dat enig drankgebruik een
prima conditie niet in de weg hoeft te staan, is er zaterdagochtend de gelegenheid
om vijf kilometer te fun-runnen.
De start is stipt om 7.15 uur in de morgen.
Deelname is gratis en als beloning ligt
er een prachtig T-shirt voor u bij de finish te wachten. Er is geen tijdslimiet,
maar u wordt vriendelijk verzocht vóór de eerste lezingen terug
te zijn.
Nationale Wiskunde Dagen 1996
De tweede Nationale Wiskunde Dagen zijn
gepland op vrijdag 2 en zaterdag 3 februari 1996. Bij het organiseren van
deze tweede Nationale Wiskunde Dagen hopen we gebruik te kunnen maken van
uw opmerkingen en suggesties naar aanleiding van de eerste Nationale Wiskunde
Dagen. Omdat wij graag willen weten wat u van de Nationale Wiskunde Dagen
vindt, ontvangt u bij binnenkomst een evaluatieboekje.
Wij hopen dat u uw opmerkingen gedurende
de twee dagen wilt noter



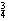 van jouw geld en ik betaal dat paard wel even.' `Nee', zegt Wouter, `leen
mij
van jouw geld en ik betaal dat paard wel even.' `Nee', zegt Wouter, `leen
mij 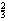 van jouw geld en ik zal het
beestje betalen.' Hoeveel geld bezaten de beide vrienden?
van jouw geld en ik zal het
beestje betalen.' Hoeveel geld bezaten de beide vrienden?
 , soms met groot nut
ook wel geschreven als Dv. In analogie daarmee kunnen de lotgevallen van discreet
veranderende verschijnselen v = vn vaak nuttig worden beschreven met behulp
van de differentie-operator Δ:
, soms met groot nut
ook wel geschreven als Dv. In analogie daarmee kunnen de lotgevallen van discreet
veranderende verschijnselen v = vn vaak nuttig worden beschreven met behulp
van de differentie-operator Δ:






