Wiskunde om de wiskunde: meetkunde
Meetkunde is helemaal terug van weggeweest. In het lesprogramma
is er weer aandacht voor meetkunde, en nu ook nog voor toepassingen van de meetkunde.
Het spel van cirkels en lijnen maakt op eenieder diepe indruk en het is voor
velen verslavend. De lezingen/workshops laten zien hoe breed de meetkunde is.
Peter Stevenhagen bespreekt een onderwerp uit de algebraïsche
meetkunde: ontegenzeglijk meetkunde, maar met vertakkingen in de algebra en
getaltheorie.
Meetkunde is van oorsprong landmeetkunde. De werking van de eerste instrumenten
van de landmeter is vaak gebaseerd op betrekkelijk eenvoudige meetkundige methoden.
De workshop van Iris Gulikers laat zien hoe dit in het onderwijs gebruikt kan
worden.
In tegenstelling tot wat velen denken, is de meetkunde, ook de gewone vlakke
meetkunde, nog lang niet af. Floor van Lamoen publiceert regelmatig nieuwe resultaten
over de gewone meetkunde en hij zal een actueel onderwerp uit de doeken doen.
Meetkunde is niet gebonden aan het vlak, de bol of de ruimte. Professor Van
der Blij zal iets vertellen over meetkunde op andere oppervlakken, zoals bijvoorbeeld
de kegel, cylinder en torus.
Factoriseren met krommen
Peter Stevenhagen
Mathematisch Instituut, Universiteit Leiden
vrijdag 13.45-14.30 uur
In de vlakke meetkunde komt men al snel in aanraking met tweedegraads krommen zoals cirkels, ellipsen en parabolen. De classificatie van dergelijke kegelsneden wordt het eenvoudigst als men ze `projectief' bekijkt en `punten in oneindig' toevoegt.
Iets soortgelijks geldt ook voor derdegraads krommen, die
we in deze voordracht zullen bekijken. Omdat een lijn door twee punten op
zo'n kromme nog een derde snijpunt met de kromme heeft, kan men een optelling
definiëren voor de punten op de kromme. De structuur van een elliptische
kromme die zo ontstaat, is ongelooflijk rijk en houdt verband met de meeste
vakgebieden binnen de wiskunde. De laatste stelling van Fermat is in 1995
met behulp van elliptische krommen bewezen en in de cryptografie worden
ze nu ook commercieel toegepast. We illustreren de veelzijdigheid van deze
krommen door er gehele getallen mee te ontbinden.
De kortste weg in andere werelden
Prof.dr. F. van der Blij
Gorssel
vrijdag 16.00-16.45 uur
Hoe kom je het snelst van A naar B? In het platte vlak is
dat via een rechte lijn. Is dat een stelling of een definitie? Het licht
kiest die weg, maar hoe zit het met de gang van lichtstralen door een lens
of een prisma?
De kortste weg van Amsterdam naar Tokio, als we geen tunnel door de aarde
willen boren, gaat via een grote cirkel op de aardbol. Maar weet je dat
wel zeker, kun je het bewijzen? Van noorpool naar zuidpool zijn vele kortste
wegen!
Als de wereld geen bol, maar een kubus of een sigarenkistje is, wat dan?
En gaat de speelse wiskunde op de loop, wat weten we van kortste wegen op
een cilinder of een kegel of een autoband?
Naast rechte lijnen spelen ook cirkels een rol bij het bepalen van afstanden,
een cirkel is immers de verzameling van alle punten met een vaste afstand
tot het middelpunt. Cirkels op de bol hebben niet één maar
twee middelpunten, hoe is dat op de cilinder en de kegel?
De antwoorden zijn verrassend en soms niet makkelijk aan te geven.
De 17e eeuwse Nederlandse landmeter in de klas
Drs. Iris Gulikers
Wiskunde en Informatica, Rijksuniversiteit Groningen
zaterdag 9.00-9.45 uur
 Waarom
zou je geschiedenis van de wiskunde in de klas gebruiken? Maar vooral: Hoe
kun je geschiedenis van de wiskunde in de klas gebruiken? Deze laatste vraag
staat centraal in deze workshop en er wordt een voorbeeld gegeven van een
project dat is uitgevoerd in tweede en derde klassen havo/vwo op verschillende
middelbare scholen in ons land.
Waarom
zou je geschiedenis van de wiskunde in de klas gebruiken? Maar vooral: Hoe
kun je geschiedenis van de wiskunde in de klas gebruiken? Deze laatste vraag
staat centraal in deze workshop en er wordt een voorbeeld gegeven van een
project dat is uitgevoerd in tweede en derde klassen havo/vwo op verschillende
middelbare scholen in ons land.
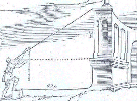
Het onderwerp van het gebruikte historische lesmateriaal is
gelijkvormigheid, dat door Nederlandse landmeters in de 17e eeuw veel als
hulpmiddel werd gebruikt. Het berekenen van de hoogte van gebouwen was een
van de werkzaamheden van landmeters, en meetkundige instrumenten als de
Jacobsstaf (zie plaatje) vereenvoudigden dit werk.
In het ontwikkelde lesmateriaal worden de leerlingen een aantal eeuwen mee
terug genomen en gaan ze zich verplaatsen in het leven en werk van de landmeter.
Het herkennen van en het rekenen met gelijkvormigheid staat centraal. Het
lesmateriaal wordt afgesloten met een praktische opdracht waarbij de leerlingen
zelf meetwerk gaan verrichten en zelf de hoogte van een gebouw gaan uitrekenen,
onder andere met behulp van de Jacobsstaf.
In deze workshop wordt een beeld gegeven van de primaire bronnen
die zijn gebruikt en vervolgens zijn verwerkt tot materiaal voor leerlingen
en docenten. Er worden voorbeelden gegeven van opgaven voor leerlingen,
maar er is eerst gelegenheid om zelf opgaven bij de gekozen bronnen te bedenken.
Daarnaast komen ook enkele ervaringen van het experiment in de klas aan
de orde. Zowel leerlingen als docenten hebben het project als leerzaam ervaren
en er met veel plezier aan gewerkt.
Meer dan een eeuw Morley
Drs. Floor van Lamoen
St. Willibrordcollege, Goes
zaterdag 10.30-11.15 uur
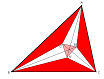 Nog
net in de 19e eeuw ontdekte Frank Morley een inmiddels beroemd geworden
stelling: Tekent men de trisectrices van de hoeken van een driehoek ABC,
dan vormen de snijpunten van de aanliggende trisectrices aan de zijden van
ABC een gelijkzijdige driehoek A'B'C' - de trisectricedriehoek van Morley.
Nog
net in de 19e eeuw ontdekte Frank Morley een inmiddels beroemd geworden
stelling: Tekent men de trisectrices van de hoeken van een driehoek ABC,
dan vormen de snijpunten van de aanliggende trisectrices aan de zijden van
ABC een gelijkzijdige driehoek A'B'C' - de trisectricedriehoek van Morley.
Deze verrassende stelling heeft veel aandacht getrokken - het is ontegenzeggelijk
een mooie stelling. Het blijkt dat op diverse manieren in de driehoeksmeetkunde
driehoeken parallel aan de trisectricedriehoek opduiken.
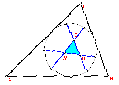 We
lopen een aantal vondsten langs, die doorlopen tot in de 21e eeuw.
We
lopen een aantal vondsten langs, die doorlopen tot in de 21e eeuw.
Wilt u vast wat lezen over de trisectricedriehoek van Morley,
dan kunt u bijvoorbeeld terecht op Alexander Bogomolny's `Cut the knot'
site:
http://www.cut-the-knot.com/triangle/Morley/
 Waarom
zou je geschiedenis van de wiskunde in de klas gebruiken? Maar vooral: Hoe
kun je geschiedenis van de wiskunde in de klas gebruiken? Deze laatste vraag
staat centraal in deze workshop en er wordt een voorbeeld gegeven van een
project dat is uitgevoerd in tweede en derde klassen havo/vwo op verschillende
middelbare scholen in ons land.
Waarom
zou je geschiedenis van de wiskunde in de klas gebruiken? Maar vooral: Hoe
kun je geschiedenis van de wiskunde in de klas gebruiken? Deze laatste vraag
staat centraal in deze workshop en er wordt een voorbeeld gegeven van een
project dat is uitgevoerd in tweede en derde klassen havo/vwo op verschillende
middelbare scholen in ons land.  Nog
net in de 19e eeuw ontdekte Frank Morley een inmiddels beroemd geworden
stelling: Tekent men de trisectrices van de hoeken van een driehoek ABC,
dan vormen de snijpunten van de aanliggende trisectrices aan de zijden van
ABC een gelijkzijdige driehoek A'B'C' - de trisectricedriehoek van Morley.
Nog
net in de 19e eeuw ontdekte Frank Morley een inmiddels beroemd geworden
stelling: Tekent men de trisectrices van de hoeken van een driehoek ABC,
dan vormen de snijpunten van de aanliggende trisectrices aan de zijden van
ABC een gelijkzijdige driehoek A'B'C' - de trisectricedriehoek van Morley.
 We
lopen een aantal vondsten langs, die doorlopen tot in de 21e eeuw.
We
lopen een aantal vondsten langs, die doorlopen tot in de 21e eeuw.